QFT is (not) hard

Yesterday was our faculty's postgrad symposium, where science students of all descriptions attempted (usually with some measure of success) to explain to science students of all other descriptions what their research is all about. This necessitates some creativity and has left me thinking (not for the first time) about whether or not QFT is indeed inexplicable. It seems worth writing up a few thoughts here.

QFT is hard.

There's a reason that nobody less than four years out of high school gets QFT (for an approximate value of nobody and allowing 'gets' to be ill-defined) and nobody with less than six years of tertiary education has actually used it in any practical way. (Again, generalisation, but I don't think it's far off the mark.) QFT is a very abstract, mathematical theory and divorcing it from the mathematics is like trying to explain swimming without water. If you want to understand QFT, come back when you have a degree's worth of mathematics. This is perhaps a little too depressing, so let's try another tack. 

QFT is not hard

Sure, the scientists who do QFT research need lots of training and deal with scary equations all day, every day, but that's not the heart of what they're doing. They're actually doing calculations on "god particles" and quarks, which are basically very small marbles glued to elastic bands which are other particles called gluons and the gluon is massless which means it's like a fish that can swim through the god particle molasses slickly, unlike the other particles, which are like whales because they have masses.

Now, I will admit that our building houses not just the physics department, but also the oceanography department and the Marine Research Institute, but we are separate departments. A quark or a Z boson is nothing at all like a whale. In fact, the work I do on a day-to-day basis involves talking about mathematical abstractions that can be experimentally tested using the ideas of such particles, but doesn't really talk about particles at all. So while I do think that non-specialists should be able to get an idea of what's going on in QFT, I'm not convinced that these analogies do much more than make people think they know what's going on. Which is perhaps worth something, but seems suboptimal.

QFT is (not) hard

QFT is an abstract theory based on abstract mathematics. If you want a genuine feeling for how it behaves, you need a genuine feeling for how maths behaves. To reuse an analogy (since I've decided they're not all bad), you can't understand swimming if you don't know what water is. QFT is related to abstract maths just as intimately and shying away from it doesn't help. But what I think we miss is that all you need is a "genuine feeling for how maths behaves". I say 'all', but of course such a feeling can be hard to come by. However, it's an awful lot easier to come by than a degree in mathematics. It almost has to be.

I don't think you need to be able to calculate a commutator to get a feel for what's going on in QFT. I do think you need to know that sometimes in maths, as in life, order matters. 2 + 3 = 3 + 2. I don't care whether you put on your hat and then scarf or you scarf and then hat. But pq is not the same as qp and you should put on your socks before you put on your shoes, unless perhaps you're going to a fancy dress party.*

For some reason we don't seem to want to explain QFT this way. Perhaps it's because we've all learned in school that maths is terrifying. Perhaps it feels like it takes us too far off topic. (I feel this every time I try to give a talk about QFT, but I find there's nothing to say if I take out the maths.) Perhaps we just haven't thought about it enough. (We almost certainly don't think about science communication enough.) Perhaps it is happening, but I'm not aware of it (and neither are my scientist friends, which would mean it needs way more publicity).

I'm still working out where  this leaves me. It means that when I talk about QFT for a general audience, I don't shy away from the maths. Maybe it means I need to write and/or talk about these ideas more often (she said, guiltily writing her first blog post in months). Maybe it's enough to be aware of it and to talk about. Maybe I need to pick fights about it. Maybe (definitely) it's not all a problem for me to solve, all on my own, today. But it's a topic that deserves some thought, in the midst of marking and debugging and trying to put in those six years you need to learn to use QFT. We'll see.

____
* I feel like a cheat putting in mathematics without explaining the physical significance. The p and q here are representing the tools we use to measure the position and momentum (which gives us the speed) of a particle respectively. The maths tells us that the order in which me measure them matters, because pq ≠ qp. This means that making one measurement must somehow corrupt the other (it doesn't tell us how that happens, sadly). This in turn means that if we measure the position correctly, we can't measure the momentum and vice versa. This is Heisenberg's Uncertainty Principle (which is one of the most obvious and well known consequences of order mattering, although not the only one). You can talk about thought experiments, like the Heisenberg microscope, to make it seem more intuitive, but it comes from the fact that if we choose maths that gives us the right answers, order matters when you write down p and q.

Definitions and Discoveries

At first glance it seems that it would be rather silly to mix up the ideas of a definition and a discovery, but at least in maths (and perhaps especially theoretical physics) it's surprisingly easy to do. Both processes produce rules that allow us to go on and derive new rules and descriptions -- the big difference is where they come from.

Might require a change of maths.

Suppose, for instance, that I want to construct a rule using the word "good". Then I would work out what the word "good" means for the rule by seeing how it works in the world -- I would discover it, rather than defining it. (There might be situations where you would choose to define it differently from how it works in the rest of the world, but you would have to be clear that you were doing something funny then.) This is rather like how we decide to write the description of gravity as pulling things together. Mathematically you could write about it as a force that pushes things apart, but that wouldn't describe the gravity we experience. Likewise, if you want to describe arithmetic as we know it, you can't decide whether 2+3 and 3+2 are the same thing. You discover that you don't get the expected results unless they are. (One might decide to define it differently anyway, but then one would no longer be talking about ordinary arithmetic.)

Things get more complicated if I have a procedure that involves putting "un" at the beginning of words. I can't go out and discover the meaning of "ungood", because it's not a word you can find in the world. Nothing about the way people talk changes if I interpret "ungood" as meaning "butterfly" or "convenient" or "pirouetting", because people don't say "ungood" in the first place. Situations like this tend to crop up in the intermediate mathematical steps of a physics problem. I've translated the situation into equations and now I want to solve them. Solving equations doesn't mean anything physically, although the solutions should be something we can translate back. That means there aren't clear physical requirements on what is or isn't allowed in trying to solve the equation. 

If I want to be able to use the "un" procedure, I have to come up with a meaning for "ungood". There's nothing stopping me from picking any definition I like -- but some will be more useful than others. I'd like to pick a definition that means the "un" procedure does the same thing it does to other rules. "Decided" becomes "undecided", "expected" becomes "unexpected" and "forgettable" becomes "unforgettable", all of which do mean things already. It makes sense that when "good" becomes "ungood", it means the opposite of "good". We might define "ungood" to mean "bad".

We don't have to define it that way, though. We could go by similar phonetics instead and define "ungood" to mean "unguent". The "un" rule wouldn't work as expected any more, of course. But if I were writing a speech-to-text program, say, that might be less important than the phonetics. Besides, it's not like the "un" rule is infallible anyway -- look at how "til" becomes "until". It's only if I want the definition to work in a system where the "un" rule always produces opposites that defining "ungood" to mean "unguent" would be inconsistent.

The same thing happens mathematically. If something doesn't exactly match up to some physical observable, we need to define what it means. Some definitions make more sense than others when it comes to translating back and those are the ones we choose. But unlike making a discovery, it is a choice. We decide that we want certain rules and procedures to do what they do elsewhere and choose to define things accordingly. The definition isn't forced upon us by the way the world works. 

Why do I care about such a subtle difference? If you just want to apply the rules, it doesn't really matter. But if you want to understand where they come from and what makes physics tick, you need to know what's required to describe the world and what's just a helpful way of thinking about intermediate maths. And that's why I'm quite sure I'm neither the first nor the last physics student to say "Oh is that just a definition? It all makes sense now..."

Savo 'lass a lalaith.

Of spin and other nonsense

From the Oxford English Dictionary:

spin:

noun 1 A rapid turning or whirling motion

 ...

1.4 Physics The intrinsic angular momentum of a subatomic particle.

...

noun 3 [in singular] The presentation of information in a particular way; a slant, especially a favourable one

I was going to write something about covering groups, which I've been reading about today, but one of the applications of covering groups in theoretical physics is in linking quantum spin to rotations. Spin is fascinating and weird. I got sidetracked.

I suspect that spin is not really all that weird, if one thinks about it properly. But in the process of discovering what exactly holds the world together, one doesn't always come across ideas in contexts that make it easy to think about them properly. Such is the case with (quantum) spin, which, despite the name, does not involve any rapid twirling or whirling motions. In fact, all the talk about twirling and whirling could probably be classified as spin in the third sense "presentation of information in a particular way; a slant, especially a favourable one" (but not necessarily an accurate one).

Spin is just a property of a particle (I'll disagree with the OED on its technically needing to be a subatomic particle, but admittedly that's overwhelmingly the context where we talk about spin.) It's easy enough to imagine a particle having a position. It can have a mass, which we tend to think about in terms of how much it weighs -- although the ideas aren't quite the same. We're happy to think about a particle having a speed. Other things are harder to imagine.

We know that there's a thing called electric charge. It's what makes lightbulbs shine and computers compute. It's the reason you can rub a plastic ruler on your head and use it to pick up scraps of paper; and the cause of thunder and lightning. It certainly seems to exist. But what exactly is it? Well, it's electric charge. If we describe it as being like something easier to imagine then we're describing it as being something different from itself.
 
There's another thing called spin. People sometimes try to describe it as whirling and twirling, because that's easy to imagine and the context in which it was first noticed. In fact, it can be linked very closely -- but not identically -- to the idea of rotations using the mathematics of covering groups. However, spin is not about twirling and whirling, so we end up describing it as something other than itself when we take that route. It tends not to end well.

There are two yellow lines in the sodium spectrum, not just one.

Spin is a thing that means splitting the light from a sodium lamp with a prism produces two yellow lines, instead of just one. There's a yellow line for each kind of spin. Spin is the thing that means if you fire a stream of particles into a magnetic field, some will go up and some will go down. It means electron energies are arranged twice as efficiently as you might expect. Like electric charge, spin has noticeable effects. Even if we can't exactly imagine it, it makes sense to talk about it.

That's where the maths comes in handy, of course -- it gives us a way to talk about things like spin, even when we don't have a convenient way to imagine what they 'actually' are.

Savo 'lass a lalaith.

I should be debugging

, but the server's down and sometimes it's good to step off the hamster wheel. I think. Maybe. It's okay to step off the hamster wheel, right? Are we allowed to admit that there is a hamster wheel?

I'm not complaining, mind you. I love my work. Really, laugh-out-loud, love theoretical physics and seeing how ridiculously, beautifully abstract mathematics can describe the real world and how things actually happen. I love C++ debugging somewhat less, but I can accept that it's part of the package. Which isn't to say it's not a bit of a hamster wheel.

On Saturday at a workshop on science communication I told an auditoriumful of people that I was infatuated with Grassman algebras. That isn't a hamster wheel. It's something to remember and savour. It's a reason to get on the hamster wheel when the wheel needs to be turned, even if I don't seem to be going anywhere.

Grassman algebras are very neat. See, ordinary numbers commute. That means you get equations like

ab - ba = 0

which is to say

ab = ba.

Five times three is the same as three times five, and for most of the things we want to use maths for, that's awfully convenient. If I switch the length and breadth of a room, I don't want the area to change! But sometimes switching things around does change things. Putting on my shoes and then my socks is not the same as putting on my socks and then my shoes.

It turns out that in particle physics there's a family of particles -- called fermions -- that behave like this. If fermion the first and fermion the second are identical (for instance, they might both be electrons), it still matters which order I put them in. No, that's not intuitive, but it does seem to be the way nature works. If I switch fermion one and fermion two, so that instead I'm looking at fermion two and fermion one, the mathematics I'm using needs to have a minus sign attached. And that's where Grassman numbers (the things you use in Grassman algebras) come in. Grassman numbers don't commute, they anticommute:

ab + ba = 0 

which is to say

ab = -ba.

In fact, Grassman numbers behave just the way fermions seem to. That means that while I might describe the length and breadth of a room using ordinary ("real") numbers, it's more convenient to describe fermions using Grassman numbers. I have to modify the rules of maths slightly to make sure that they anticommute, but otherwise I can carry on just as before. The kind of number I'm using does most of the work and I don't have to keep accounting for the odd behaviour of fermions. The fact that they do strange things when you swap them around is built in.

 I think that's pretty. Just about pretty enough that I might muster the willpower to go and ask C++ why it insists that the solution to my equation is infinity. (The solution is not infinity. Unless I've given it the wrong equation. Or the wrong method for solving the equation. Or I accidentally typed +∞ before printing the answer. Maybe I'll go check that last one.)
-----
Savo 'lass a lalaith.

Patterns

 Some correlations without much thought on the mechanisms behind them. Things I've noticed. 


Three participants at the Cape Town heats of the FameLab science communication competition prepared their talks for both regional rounds before the day. (The others prepared the second talk during lunch break.)
//
The same three participants were the three sent through to the national stages.

(Did they [we] do better because they [we] were more prepared, is there something that affects both or is it just chance?)


Researchers are evaluated not by what they understand (which is hardly measurable), but by "research output" or publications.
//
Students are told that it's more important to understand the topic than to worry about the grades.

(This is partly to do with what we can measure and partly to do with how we look at things and definitely a question that goes much deeper than what I've written here.)





If I get to  bed early, I'm much more capable of being productive in my work the next day.
//
A lot of fun-sounding events are run in the late evening.
//
There's a stereotype about scientists not having social lives.

(Even the most obvious way of linking these doesn't involve social awkwardness. One might argue that it implies it, I suppose.)


Mathematica is probably* the most expensive and widely-used symbolic programming language out there.
//
It also has the best pattern matching capabilities.*

(My supervisor likes to point out that, even so, it's a terrible stand-in for your brain.)



*I've heard so and it sounds plausible, but I haven't looked it up for myself.

Not-Friday Five

1. We cooked spaghetti and meatballs for supper Friday night and it turned into a fancier meal than I expected. I'm not sure if it was because making meatballs is a little more effort than I usually go to or just Friday night fanciness or some happy serendipity, but it reminded me that cooking can actually be fun. I need to find more time and energy for that on a regular basis.

2. Quantum physics is weird. Niels Bohr (one of the founders of the subject) once (somewhat) famously said that "Anyone who is not confused by quantum mechanics has not understood it." This makes for some really cool stuff, but also makes it tricky to tell whether there's a typo in your notes or things really are just that weird.

3. I spent quite a while persuding the campus bookstore to source books from the suppliers for me. The online people would do it happily, but they couldn't process the gift card I'm using to finance the purchases. However, I now have a couple of books I've been wanting to read - that weren't even on special - on the way. This is exciting!

4. My siblings have all attended schools that presented book vouchers with academic awards, but I never did. I feel like part of the club now that university's doing it too.

5. Wednesday was a public holiday. It was wonderful to have a day off from classes, and while chunks of it were filled with homework, other chunks were filled with a tie-dye project It was fun! I could get addicted to this stuff.

FameLab

I missed my Wordless Wednesday post this week and then I missed my Friday Five too. And I've started reading The Return of the King without blogging about The Two Towers. I could probably blame my honours quantum mechanics course or my insistence on making the wraps we had for dinner from scratch, but I'm going to pin it on FameLab instead.

FameLab is an international event/competition that promotes young scientists "Talking Science" with the general public. Conversely, it promotes people hearing - and hopefully learning - about science, which is a Good Thing in my book. It's all done through the form of three minute presentations where PowerPoint slides and more props than you can carry are banned. This works really, really well, despite its simplicity.

For one thing, "Death by PowerPoint" and related maladies were almost entirely banished. For another, three minutes is barely long enough to get bored. The time limit was strictly enforced by vuvuzela (I assume other countries have equivalents) - although just the threat seemed enough for the people I watched. Regional heats were open to any (practising or studying) scientist in the 21-35 age range, which seems to have ensured that everyone had something worth saying - and not enough time to make it boring.

There was feedback from the judges after each presentation - I was impressed at how much this stayed positive, helpful and interesting to the audience. Presenting and being scrutinised was a little scary - the cameramen and microphones and masking tape squares on the floor didn't help - but an awesome experience.

A handful of us were invited back to regional finals - another three minute presentation a couple of hours later, taking into account the judges' feedback. The fact that it had to be a different presentation seems like a rather effective test of breadth. It felt like a test of improv skills too when we were suddenly called for on-camera interviews! It's surprisingly tricky to do that sit-sideways-and-smile-at-the-camera drill, never mind actually answering questions! Not that I'm complaining: it was all part of the excitement.

The regional finals were awesome. While some of the first round presentation were a bit rough, these were all fascinating. The kind of thing that would make for a great school field trip or the like, I thought. The scientific basis for the zombie apocalypse; a eulogy for coal; forensics and DNA testing. (You can see something of the impressive breadth the presentations covered there too.)

My nails probably owe their continued existence to all the interesting people I had to talk to while the judges deliberated, between the scientists and the competition staff. The compere seemed less friendly when she started stalling the results, though . . .

Three of us went through to the national finals. One of them was me! Um, what? I entered this thing just for kicks - the first round really is an experience in itself (next year I'll be telling everyone else to do it too). I'm just this girl who likes showing people how things work, not some kind of professional anything.

But apparently I'm going SciFest Africa in Grahamstown. I think. If I were dreaming I would've woken up by now, right? And it wouldn't have left me so ridiculously tired.

Things they said

Discussing Lent at Sunday School, we mentioned doing things like giving up chocolate or taking up reading your bible. So one little girl asked "Can I eat chocolate every day for Lent?" Uh, not quite.

Also at Sunday School, one seven-year-old didn't like the way a game was being played. So she marched over to her own game and announced "I'm going to play this in the third person."

In my other natural habitat, the physics department, from a grad student who's competent in such mathematical topics as multivariate calculus and tensor analysis: "Why do minus signs have to be so confusing?"

And on the blackboard after a lecture involving the emission of UV light: "the ultra-violent catastrophe". Guess Max Planck was more of a hero than I thought!

Savo 'lass a lalaith.

Research

Today while I was talking to Sir Laughs-a-lot, because this is apparently what grad students do, we formulated an algorithm for research. I, uh, decided the world would be a better place for my putting on the internet. So here goes.

1. Get confused. (We totally have this one nailed. But as Sir L says, it can be fun.)

2. Get unconfused. (Easy, right?)

3. Write a paper. "Look! I'm unconfused, look at me! You can be unconfused too."

4. Win Nobel prize; become rich and famous (optional).

We were doing step two for a thermodynamics problem which has technically already been solved, but only by other people and we ended up with a (hypothetical) balloon that filled the whole universe. This is why I'm studying physics.

Trends and Community

Exams are finished! I'm not sure it's possible to adequately express my glee about this in writing. I am not an exam person. (Lest you think that redundant, let me assure you that I have on occasion met people who do handle exams with poise and grace.) Presently I will go home, see my family and laze around reading analysis textbooks. In the meantime, I am working at university, which is quite* cool.

The work I'm doing involves going way back through the archives of academic journals and sorting out which papers are relevant for one of my lecturer's projects. One of the side-effects is that I get to see a little bit of the flow of physics research over time.

It's weird to see the papers people were writing when I was still learning to read, all put together in a sort of conversation. It's no surprise that people were doing physics when I was a kid (I've certainly used papers from way before I was born before), but it is a little odd to find this community that I can never really know preserved in the pages (or pdf files) of the Am. J. Phys.

It's also interesting to see how different topics go in and out of vogue. There's always a certain amount of mechanics, quantum physics, electromagnetism and so on, but there are time periods when certain things crop up repeatedly and quite frequently. For instance there were a couple of years that saw a cluster of papers about the charge on a magnetised needle; during another phase it seemed quite fashionable to deal with surface tension problems. I think it's fascinating that such trends exist.

I'm not sure if these patterns have much direct practical application, but I do think they're useful in getting know physics. I recall once reading somewhere that before trying to participate in an internet forum, it can be helpful to 'lurk' and see how things are done there. I guess the academic equivalent is reading all the way back through the journal archives.
_____________________
*Where 'quite' means 'extraordinarily, but that seems potentially like an over-the-top response, so I'll just say quite,'

Thinking like a physicist

@mathematicsprof on Twitter recently tweeted a link to a page asking what it's like to understand advanced mathematics. There are a number of very interesting answers there, but one interested me particularly. I can't figure out if there's a way to link to it directly, but I'll quote it here:

From Jack Miller:

 

A two part question to determine if you "think like a mathematician," from Prof. Eugene Luks, Bucknell University, circa 1979.

Part I: You're in a room that is empty except for a functioning stove and a tea kettle with tepid water in it sitting on the floor.  How do you make hot water for tea?
Answer to Part I: Put tea kettle on stove, turn on burner, heat until water boils.

Part II: Next, you're in another room that is empty except for a functioning stove and a tea kettle with tepid water in it sitting on a table.  How do you make hot water for tea?
Non-mathematician's answer to Part II: Put tea kettle on stove, turn on burner, heat until water boils.
Mathematician's answer to Part II: Put the tea kettle on the floor. 

Why?  Because a solution to any new problem is elegantly complete when it can be reduced to a previously demonstrated case.

 This might be why I'm studying physics more than maths. I can see why putting the kettle on the floor solves the problem rather elegantly - I think it's a nicer solution than the "non-mathematician's answer" up there - but it's not how I would solve the problem. Isn't it obvious that the table is negligible in this situation, so that Part II is reduced to Part I?

Mathematicians aren't, I think, supposed to say things are negligible. Assuming that the table is negligible isn't rigourous. It does, however, get to the right solution without (explicitly, at least) going via the floor. It's still elegant (if you can get over the idea of neglecting the table) and it takes less effort.

Perhaps it's related to the idea that physics is not so much about working out how to describe some given bit of the universe as it is about working out which bits of the universe we can describe and doing so. This is usually expressed in terms of finding symmetries, from what I've seen and heard. Here, I think the system is invariant under the introduction of the table, which is a symmetry.

There are probably other ways of solving the problem, too. I think it's a very interesting exercise in how people think!

With Recurring Kittens

One.

I wrote my first exam for this semester yesterday. I think it went reasonably well; it was oddly satisfying to throw out the thirty-plus pages of notes I'd generated over the last few days. (Not the actual notes I made in class - I keep those. But I tossed the duplicates that ensured the class notes did actually (mostly) transfer to my memory.) There is now some danger that I begin to feel that having worked so hard for that course, I needn't worry about the others. Which would be foolish. To combat this assumption, I'm going to try to finish a section of Quantum Mechanics between writing each take here. (I'm stealing the general idea from here.)

Two.

I came across this writing competition yesterday, which asks for writing inspired by Benjamin Franklin's quote "If you would persuade you must appeal to interest rather than intellect." Now, physics is indubitably awesome because it allows us to harness the power of mathematics to understand the nature of the universe. It's pretty cool that way. But part of the fun - especially, perhaps, when it comes to revision - is things like my Q.M. lecturer's comment that there are physics-loving kittens who cry every time students try to explain the uncertainty principle without explicitly stating that it's fundamental. Doesn't sound plausible, you say? Well neither does quantum mechanics.

I don't think those two ideas are properly linked up there. If I figure out how to link them properly, I might have a competition entry.

Three.

I am going to use part three to write about the idea of determinism in classical mechanics so that I can refer to that idea in part four. It's pretty interesting for it's own sake too, though. Determinism starts with the sort of idea that if I know that a train leaves the station at two o'clock and travels at a constant speed of 60 km/h (I have no idea how fast trains actually travel) in a constant direction, I can tell you exactly where it will be at three o'clock. Of course, the train needn't travel at a constant speed in a constant direction, so I could  be quite wrong. When it comes to Newton's laws of mechanics, however, the only thing that can cause a particle to change its state of motion is some kind of external force (that's basically Newton's first law). So if I know all the particles and all the forces they can exert, I can work out everything that will happen. This raises some rather interesting questions about free will, since although practically nobody could know what every single particle in the universe is doing, the idea that it's theoretically possible is rather creepy. Quantum mechanics saves the day here, though: it turns out that even theoretically it's not possible to know everything about even one particle. Of course, that's rather weird in its own right.

Four.

This painting is awesome.

Il castello di Bentheim (Jacob Van Ruisdael)

I don't think you can explain why a painting is awesome by describing particles that fly around colliding and absorbing one another. They can be deterministic classical particles or random quantum particles, but they don't explain things like beauty. Or truth. (You can talk about my perception of truth in terms of particles in my brain, perhaps, but not about truth itself.) And they're not supposed to. That's why physics isn't metaphysics. It's kind of obvious in some ways and awfully hard to hold onto in others. Part of the appeal of physics (apart from the kittens) is trying to understand things. We understand more and more stuff, at a more and more fundamental level, as we go on, but at some point, in some directions, it has to stop working. Which is just as well, on the whole, but can be a little disappointing in the moment.

Five.

 It is a mark of something, I'm sure, that I've quite lost track of my reading list. Probably the amount of work involved in a final year maths/physics course. I don't actually know if I've read (well, finished) anything (that's a book) since Silver on the Tree, although I suspect I haven't. And I don't remember exactly when I read that, so that it's an altogether sorry state of affairs. However, in my efforts to do something meaningful and productive that does not involve calculating the probability amplitude function for a particle on a ring for the umpteenth time, I realised that my average reading rate for the year is still a book a week. And I definitely read more academic papers than I used to, which ought to count for something. Perhaps not altogether a sorry state of affairs, then. But it's rather odd to say that I can't remember the last time I finished reading a book.

Six.

Do you still remember the physics-loving kittens? I suggested that such a thing might be implausible, but through the wonders of Google image search and The Particle Zoo, I have now found such kittens. Behold:

You can click the image for more quarky quirky physics humour with kittens.

If you have not encountered The Particle Zoo before, it's where you go to buy a universe in a box. No, seriously.

Seven.

And that's that. I did not study a section of quantum mechanics between each post, because I couldn't make up my mind about how to define a section. So I did some studying and some writing and it all got mixed up together. As long as I don't start drawing kittens in my exam paper, I think that's okay. I missed the boat for keeping quantum mechanics off the blog a while ago.

Redefining Survival Mode

Every once in a while one is forced to go into survival mode, I think. It's simply not possible to do everything that one would like to, or even to do most of it altogether properly. So one ends up doing an okay job of the critical stuff until things improve. For instance, I may or may not have recently been heard to say 'I don't understand that, but it doesn't matter -- it's not in the exam.' It's not that I don't care about understanding things. It's that I have a fairly good argument for understanding the things that are in the exam first.

However, I've noticed that my definition of what exactly constitutes this survival mode seems to be changing. Survival mode used to mean sitting and staring tiredly at my cup of tea instead of getting on with my work. Now I sit and stare tiredly at my cup of tea, contemplating the curl of the tea velocity field and wondering if heat transfer would affect that velocity field. And what would the scalar heat field superimposed (as a colour map, say) on the velocity field look like? And if heat flow was treated as a vector? I may even pull up something like Mathematica or Gnuplot to get an idea of what those things would look like. All this still instead of the work I'm supposed to do, although I won't take it any further than that.

It still feels like survival mode, but it seems qualitatively different from the other kind of survival mode. I'm not quite sure where it comes from. Perhaps it's the increased 'mental fitness' after a couple of years of university maths and science; a gradual change in the way I think about things that's just highlighted by the fact that I'm survival mode-ing. Perhaps half a dozen things. I'd need to create an ensemble of identical systems and observe their evolution over time to be sure.

Whatever the cause, I think it's a kind of interesting phenomenon. I should probably stop staring tiredly at the computer screen and go figure out how to use a Cornu spiral, though.

This describes Fresnel diffraction. I'm still figuring out how.

I like bullet points

• It's somehow less intimidating to write a bunch of not necessarily related points out of whatever vaguely interesting soup is floating around in my head than to pound out a nice set of linky paragraphs with a common theme. Let's not talk about why I might intimidate myself about posting to my own little blog in this corner of the internet. Test season and rationality do not have a high level of overlap.
• Let's not talk about test season either. I'd rather tell you that I started listening to the Math/Maths podcast and it's really awesome. Also, it makes me feel like I should actually remember to write about mathsy physicsy stuff on here more often. I thin we can call that a double win. The podcast assumes you know a little bit about maths (or math, for the Americans), but it certainly doesn't expect you to be at research level in anything. I like listening to something with a bit of meat to it without feeling like I've bitten off more than I can chew!
• I'm not sure whether or not that was a mixed metaphor.
• I've finished the first two of my final year courses! Our computational physics courses are largely based around actually writing code, so there's no final theory exam. The general consensus is that continuous assessment is actually more work than otherwise (I write a three hour theory exam for my 16 credit theoretical courses; I wrote a four hour final practical test for an 8 credit computational course), but it's lovely to be finished already!



Hydrogen molecule ion orbitals.

We get to make pretty pictures in comp. phys. too. Like this one, showing the electron orbitals (where the electron is most likely to occur) of a hydrogen molecule ion. This one was done in Mathematica, which is a wonderful tool for crunching through maths that's technically doable but not very much fun. Also, it draws pretty pictures.

(I haven't taken the care with formatting that I would in a proper report, so if there's anything odd about the image, that's probably why! You can look up molecular orbitals or the linear combination of atomic orbitals model if you're really interested in seeing the science done properly.)

• We spent some time yesterday trying to get Mathematica to draw rank two tensors for us, before realising that it was a rather silly idea. A rank zero tensor is just a scalar, or point on the number line, so it's pretty easy to understand. A rank one tensor is a vector (in R³), which you can visualise as an arrow in three dimensional space. A rank two tensor maps one three dimensional vector to another, which means, as far as I understand it, that you'd need a nine-dimensional blackboard to draw it out. Unfortunately (or perhaps fortunately), Mathematica doesn't have a Plot9D command. I can't imagine why not.
• One of the best parts about getting this far into my degree is that as a class we both know each other well enough and are sufficiently interested in physics that between lectures we (sometimes!) do stuff like trying to draw (potentially impossible) things in Mathematica or work out the details of a proof we glossed over in class. See also: hitting 'random' repeatedly on xkcd, and looking at graphs showing that the exponential growth rate for yoghurt is higher than that of gingerbeer or sourdough by a ridiculous amount.
• Are there physicsy versions of things like Math/Maths and Aperiodical? I can find stuff about science-in-general or maths-in-particular easily enough, perhaps because I already know where some of it is, but physics-in-particular doesn't seem to be very well represented. I don't know if maths gets more attention on it's own because it's sometimes excluded from 'science', if it's just considered more awesome than physics or if I just happen to have stumbled upon the online maths community and have yet to discover the physicsy* analogue.
 

*I have now used 'physicsy' three times. This makes it a real word. To quote the estimable Lewis Carroll (in The Hunting of the Snark) "I have said it thrice: // What I tell you three times is true."

Numerical Analysis on a Calculator

Today in my differential equations class, we ended up trying to solve the equation x=cos x. And couldn't. Well, I'm not sure everyone was trying very hard, but I had scribbled trig identities all over my page without making any progress whatsoever. Eventually the lecturer took pity on us (or decided that giving us any longer was a waste of his time, perhaps!) and told us to take out our calculators. Oh! So all that analytical fiddling wasn't helpful. It's quite easy to solve the equation numerically on a pretty standard scientific calculator, though, and quite a pretty technique too, I think. I thought I'd share it.

Pick any number you like. If you pick it close to the right answer, the process will be a little quicker, but it doesn't really matter. From the picture below (drawn with Gnuplot), 1 seems like a reasonable starting point.

Now you put cos(1) into your calculator. You don't get 1 back out, so that's not your solution. But if you take cos of that answer, and then cos of that answer and so on for a little while (you can probably do something like just hitting '=' over and over) the answer eventually stops changing. You've found a value which - at least to the accuracy your calculator displays - is it's own cosine. That's the solution. Quite neat! (I think that method is the numerical form of Picard integration, but I could be quite wrong.)

Having started playing with Gnuplot, I don't want to stop, so before I go back to work, why don't I show you a picture of the probability densities we're calculating for the particle-in-a-box problem? It's pretty, at least.

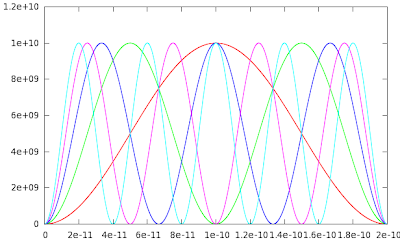Probabilities of finding an electron at different points in an infinite potential well for five different energy states. (I hope.)

Seven Quick Takes

One
  The thing about living in a UCT+2 timezone is that by the time I see people posting about Friday, it's well into Saturday for me. Or maybe it's just a problem because I follow a lot of international American blogs. Or maybe it's just that I'm not organised enough. At any rate, the last couple of weekends have seen me scrolling through my feedreader saying 'Oh, I guess it's too late to write one of those 7QT posts'. But it looks like I might've pulled it off this time.

Two
  It's not that I'm a perfectionist or anything. I completely accept that nothing will be done 100% right. I'd just like everything to be within a few standard deviations of correct. 3-sigma certainty, for example, is 99.7%. A 0.3% error in the posting time would give me, um, less than four and a half minutes into Saturday when I could post. See? Totally not perfectionist about stuff. Not whatsoever.

Three
  The holidays are too long. Now, people will object if I advocate for more term time, but I think it would be cool if we could take a couple of weeks from the long summer/winter holidays and tack them onto the ridiculously short mid-semester breaks. It might be nice to have a more balanced kind of year, but it would definitely be nice if I didn't have time to realise that the sensible thing to do with my curriculum might be to pick up Operations Research and Numerical Methods and drop Real Analysis and Algebraic Structure. I think it's worth struggling to take the courses I'll most enjoy, though.

Four
 It's not that the other modules are horrid, but it feels like switching waffles and ice-cream for macaroni and cheese. Macaroni cheese is yummy and good for you, but, well, it's not waffles and ice-cream.

Better than macaroni cheese? [Photo by Michael Kwan]

 It's kind of hard to justify that, though. The applied maths courses would probably open more doors for me in terms of postgrad studies and the fact that they don't clash with my required physics courses is probably also significant. The pure maths courses look like more fun. And given that I don't really know what I want to do next year, I can't base my decisions on that. But it's not worth stressing about till I'm back on campus. So really, the holidays should just be shorter.

Five
 When I'm trying not to stress (for whatever collection of reasons) I read. A lot. In the last few days I've read Northanger Abbey as well as all five books in Rick Riordan's Percy Jackson and the Lightning Thief series. Riordan is awesome, but I couldn't help noticing that Percy dreams an awful lot in those books. Dreams are used as a really cool plot device, but given the number of throwaway comments the guy makes about his past dreams, he must have way more non-plot-related dreams than plot related ones. But he says he dreams way more at camp (where the action happens) than elsewhere. The epistemo-temporal maths doesn't work out. (It's still better than Harry Potter, where there are forty kids per year, but six or seven hundred in the school . . .) Despite such things, I love the books.

Six
 No, I don't think epistemo-temporal is actually a word. But let's pretend and use our etymological detective skills, yes? Epistemo from the Greek word ἐπιστήμη (epistēmē), meaning "knowledge". Temporal from the Latin root tempor- meaning "time". That is, the knowledge Percy gains by dreaming doesn't seem to tie up with the amount of time he spends dreaming. And I feel totally justified in mixing Latin and Greek, since Riordan does it all the time, although we hardly noticed until it became the premise for the new Heroes of Olympus series.

Next on my (re)reading list (anyone who writes about classical mythology set today with a steampunk edge has to be pretty awesome, right?)

Seven
 There is a blog called Faraday's Cage is where you put Schroedinger's Cat.

 It reminds me of why engineering is awesome, as well as why it frustrated me. It makes me think it doesn't really matter that much which bunch of cool courses you take for your undergrad degree: you can still shift around a bit more later if you're willing to work. It's pretty cool if you're interested in stuff like Physics/Maths/Engineering/Science Education/Gifted Child Education/Homeschooling/Cute Fluffy Animals*. I saw it featured here and it's part of the reason The Lost Hero is still on the to-be-read list (rather than the currently-reading list).
___
*Actually, it's pretty cool even if you aren't, but you probably have to like some of them to enjoy it.