Numerical Analysis on a Calculator

Today in my differential equations class, we ended up trying to solve the equation x=cos x. And couldn't. Well, I'm not sure everyone was trying very hard, but I had scribbled trig identities all over my page without making any progress whatsoever. Eventually the lecturer took pity on us (or decided that giving us any longer was a waste of his time, perhaps!) and told us to take out our calculators. Oh! So all that analytical fiddling wasn't helpful. It's quite easy to solve the equation numerically on a pretty standard scientific calculator, though, and quite a pretty technique too, I think. I thought I'd share it.

Pick any number you like. If you pick it close to the right answer, the process will be a little quicker, but it doesn't really matter. From the picture below (drawn with Gnuplot), 1 seems like a reasonable starting point.

Now you put cos(1) into your calculator. You don't get 1 back out, so that's not your solution. But if you take cos of that answer, and then cos of that answer and so on for a little while (you can probably do something like just hitting '=' over and over) the answer eventually stops changing. You've found a value which - at least to the accuracy your calculator displays - is it's own cosine. That's the solution. Quite neat! (I think that method is the numerical form of Picard integration, but I could be quite wrong.)

Having started playing with Gnuplot, I don't want to stop, so before I go back to work, why don't I show you a picture of the probability densities we're calculating for the particle-in-a-box problem? It's pretty, at least.

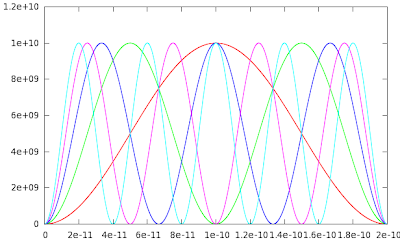Probabilities of finding an electron at different points in an infinite potential well for five different energy states. (I hope.)

Details

Despite appearance, I am neither dead nor gone. I'm landing. Working out how to cook for two. Working out how four people with three cars can share a single garage. Hoping that the university internet will be a little more reliable once the registration hordes have faded.

Lectures start on Monday morning. In preparation, I have worked out my timetable. I haven't worked out my lecture venues yet. Or labelled my files. Or actually registered for the extra elective which is making my timetable look as scary as it does. (There are six timetable blocks, running 07:45 - 17:30, Monday to Friday. I have  courses in five of those blocks.) I most certainly haven't looked over last years notes so that I'm ready to pick up where we left off, or more than half thought about doing that so-lauded preparatory reading for any of my courses.

Probably, none of that is necessary. Certainly, it's more important that I know how to work the kitchen of the house we're staying in, that I've got the best route from the fridge to the supermarket and back worked out, that I've met the lovely people who are helping our church youth group get organised again, that I'm working out how to do the things I do 'just for fun', but which are really rather important to my sanity.

So tonight I'm going to work out how to make handwritten file tags look just as snazzy as computer-designed ones. I'm going to work on the Baltic myth I'm retelling for a deviantART contest/project. (I don't expect to win, but I want to enter anyway.) I'll have a go at cooking for one, since my sister and partner-in-crimeooking is going out.

Nothing fancy; nothing tragic; nothing exciting, perhaps. But life is taking shape. Sometimes the drama is in the details.